El Perceptrón – Redes Neuronales: La Primera Piedra

Imagina un cerebro diminuto, una célula digital que puede aprender a tomar decisiones simples. Eso, en esencia, es un perceptrón, el héroe olvidado que sentó las bases de las potentes redes neuronales que hoy impulsan la inteligencia artificial. No te asustes con los términos técnicos; vamos a desglosarlos pieza por pieza hasta que todo encaje.

Perceptrón y Redes Neuronales

Piensa en tu propio cerebro. Está compuesto por miles de millones de neuronas interconectadas que se comunican entre sí. Cuando ves un perro, ciertas neuronas se “activan” de una manera específica, permitiéndote reconocerlo. Las redes neuronales artificiales son una simplificación de este proceso biológico. Son sistemas computacionales inspirados en el cerebro que pueden aprender de los datos, identificar patrones y tomar decisiones.

El perceptrón es la neurona más básica de estas redes. Es la unidad fundamental que recibe información, la procesa y emite una señal de salida. Una neurona artificial que toma varias entradas, las pondera y produce una salida binaria (0 o 1). Antes de ver el perceptrón, asomémonos a las herramientas matemáticas que lo hacen posible: vectores, matrices y el producto escalar.

Entendiendo los Vectores

Un vector es simplemente una lista ordenada de números. Puedes pensar en él como una flecha en el espacio que apunta a una ubicación específica. Vector: una lista ordenada de números. Ejemplo: v = [2, –1, 4].

• Nuestras entradas forman un vector: X=[x1​,x2​,x3​]
• Nuestros pesos forman otro vector: W=[w1​,w2​,w3​]

Perceptrón: Entradas, Pesos y Salida

Imagina nuestro perceptrón como una balanza inteligente.

Entradas (Inputs): Son los datos que le damos al perceptrón. Piensa en ellas como diferentes características o “pistas” sobre algo. Por ejemplo, si queremos que nuestro perceptrón decida si una fruta es una manzana, las entradas podrían ser:

• Forma (¿redonda?)
• Color (¿rojo o verde?)
• Tamaño (¿pequeño/mediano?)

Cada entrada es un número. Podemos representarlas como un conjunto de números: [x1​,x2​,x3​,…,xn​].

Entendiendo las Matrices

Una matriz es una colección rectangular de números, organizada en filas y columnas. Piensa en una tabla de datos. Un arreglo bidimensional de números (varios vectores apilados)

En una red neuronal multicapa, podemos representar todos los pesos entre una capa y la siguiente como una matriz. Esto permite realizar cálculos muy eficientes utilizando multiplicación de matrices, que es una generalización del producto escalar. Cada columna de la matriz de pesos podría representar los pesos para un perceptrón específico en la siguiente capa. Ejemplo:

M = [[2, -1, 4],
     [1,  0, 3],
     [5,  2, 1]]

¿Para qué sirven?

• Representar datos de entrada (vectores)
• Pesar esas entradas (vector de pesos)
• Hacer operaciones con muchas neuronas a la vez (matrices de pesos)

Pesos (Weights): Aquí es donde la “inteligencia” del perceptrón comienza a manifestarse. Cada entrada tiene un peso asociado. Piensa en los pesos como la “importancia” que el perceptrón le da a cada pista.

• Si el color rojo es muy importante para identificar una manzana, el peso asociado al “color rojo” será alto.
• Si el tamaño no es tan importante, su peso será más bajo.

Estos pesos son números que el perceptrón aprende y ajusta con el tiempo. Los representamos como otro conjunto de números: [w1​,w2​,w3​,…,wn​].

Sesgo (Bias): Es como un “umbral” adicional o un “empujón” que el perceptrón puede tener. Nos ayuda a ajustar la salida incluso cuando todas las entradas son cero. Piensa en ello como un valor predeterminado que siempre está ahí, independientemente de las entradas.

El Proceso Interno del Perceptrón

Ahora, veamos cómo el perceptrón redes neurales que toman una decisión. El corazón del perceptrón es una operación simple pero poderosa:

• Paso 1: Multiplicar y Sumar (El “Producto Escalar”)

El perceptrón toma cada entrada (xi​) y la multiplica por su peso correspondiente (wi​). Luego, suma todos estos productos y le añade el sesgo (b). Imagina que tenemos dos entradas (x1​,x2​) y sus pesos correspondientes (w1​,w2​) y un sesgo (b). El cálculo sería:

Resultado=(x1​∗w1​)+(x2​∗w2​)+b

Este paso es crucial y aquí es donde entran en juego los vectores y el producto escalar.

Producto escalar

El producto escalar (o dot product) entre dos vectores v y w de la misma longitud es la suma de multiplicar componente a componente:

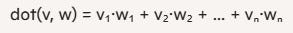
Ejemplo:

v = [2, -1, 4]
w = [1,  3, 0]

En el perceptrón, este valor decide si la neurona “dispara” (1) o no (0).

En otras palabras, nuestro producto punto es una operación matemática entre dos vectores que produce un único número. Es exactamente lo que hicimos en el Paso 1:

Para dos vectores A=[a1​,a2​,…,an​] y B=[b1​,b2​,…,bn​], el producto escalar es:

A⋅B=(a1​∗b1​)+(a2​∗b2​)+…+(an​∗bn​)

Entonces, el “multiplicar y sumar” dentro del perceptrón es en realidad el producto escalar entre el vector de entradas y el vector de pesos. Esto es increíblemente eficiente para procesar datos.

Por lo tanto, el cálculo del perceptrón se puede expresar de forma compacta como:

Resultado=(X⋅W)+b

• Paso 2: La Decisión (Función de Activación)

Una vez que el perceptrón ha combinado sus entradas con sus pesos y el sesgo, el resultado pasa por una “función de activación”. Esta función es como un interruptor. Para el perceptrón original, esta función era muy simple:

• Si el resultado supera un cierto umbral (por ejemplo, cero), el perceptrón se “activa” y emite un 1.
• Si no lo supera, emite un 0.

Es decir, una vez que tenemos el Resultado, el perceptrón lo pasa por su función de activación. Para el perceptrón original, esto es una función escalón o de umbral:

• Si Resultado≥Umbral (o Resultado≥0 si el umbral está incorporado en el sesgo), la salida es 1.
• Si Resultado<Umbral, la salida es 0.

¡Y eso es todo! El perceptrón ha tomado una decisión. Es una decisión binaria: sí o no, 1 o 0.

El perceptrón paso a paso

1. Entradas: x = [x₁, x₂, …, xₙ]
2. Pesos: w = [w₁, w₂, …, wₙ]
3. Sesgo (bias): un número b que desplaza la frontera de decisión
4. Cálculo interno: z = dot(w, x) + b
5. Función de activación (step): y = 1 si z ≥ 0, y = 0 si z < 0

Este simple esquema aprende a clasificar datos linealmente separables.

Ejemplo de Implementación básica en Python (sin librerías)

# perceptron_simple.py
import random

class Perceptron:
    def __init__(self, n_inputs, lr=0.1):
        # Inicializamos pesos al azar y sesgo en 0
        self.weights = [random.uniform(-1, 1) for _ in range(n_inputs)]
        self.bias = 0.0
        self.lr = lr  # tasa de aprendizaje

    def activation(self, z):
        # Función escalón
        return 1 if z >= 0 else 0

    def predict(self, x):
        # Producto escalar + bias
        z = sum(w * xi for w, xi in zip(self.weights, x)) + self.bias
        return self.activation(z)

    def train(self, training_data, epochs=10):
        # training_data: lista de (entrada, etiqueta)
        for epoch in range(epochs):
            for x, target in training_data:
                y = self.predict(x)
                error = target - y
                # Ajuste de pesos y bias
                for i in range(len(self.weights)):
                    self.weights[i] += self.lr * error * x[i]
                self.bias += self.lr * error

# Ejemplo de uso: puerta lógica AND
if __name__ == "__main__":
    # Datos AND: entradas y salidas esperadas
    data = [
        ([0, 0], 0),
        ([0, 1], 0),
        ([1, 0], 0),
        ([1, 1], 1),
    ]
    p = Perceptron(n_inputs=2, lr=0.2)
    p.train(data, epochs=20)

    # Probamos
    for x, _ in data:
        print(f"{x} -> {p.predict(x)}")

Explicación:

• self.weights: lista de pesos w₁…wₙ
• self.bias: sesgo b
• En cada muestra calculamos y, comparamos con la etiqueta target y actualizamos:
• wᵢ ← wᵢ + α·(target–y)·xᵢ
• b ← b + α·(target–y)

Ejemplo Usando NumPy para vectores y matrices

import numpy as np

class PerceptronNumpy:
    def __init__(self, n_inputs, lr=0.1):
        self.weights = np.random.uniform(-1, 1, size=n_inputs)
        self.bias = 0.0
        self.lr = lr

    def activation(self, z):
        return np.where(z >= 0, 1, 0)

    def predict(self, X):
        # X puede ser matriz: cada fila es un ejemplo
        z = X.dot(self.weights) + self.bias
        return self.activation(z)

    def train(self, X, y, epochs=10):
        for _ in range(epochs):
            y_pred = self.predict(X)
            error = y - y_pred
            # Vectorizado:
            self.weights += self.lr * X.T.dot(error)
            self.bias += self.lr * error.sum()

# Ejemplo AND
X = np.array([[0,0],[0,1],[1,0],[1,1]])
y = np.array([0,0,0,1])

p = PerceptronNumpy(n_inputs=2, lr=0.2)
p.train(X, y, epochs=20)
print(p.predict(X))  # [0 0 0 1]

Ventajas de NumPy:

• X.dot(self.weights) calcula todos los productos escalares de golpe.
• Operaciones enteramente vectorizadas, mucho más rápidas.

¿Cómo Aprende el Perceptrón?

Al principio, los pesos y el sesgo del perceptrón son aleatorios. Por lo tanto, sus decisiones serán probablemente incorrectas. Aquí es donde entra el aprendizaje. El perceptrón aprende a través de un proceso de prueba y error, ajustando sus pesos y sesgo para tomar mejores decisiones.

1. Ejemplo de Entrenamiento: Le mostramos al perceptrón un ejemplo (por ejemplo, una imagen de una manzana) y le decimos cuál debería ser la salida correcta (1, porque es una manzana).
2. Calcular Error: El perceptrón hace su predicción (digamos, 0). Comparamos su predicción con la salida correcta. ¡Hay un error!
3. Ajustar Pesos: Si el perceptrón se equivocó, ajustamos los pesos y el sesgo.

• Si la salida esperada era 1 pero el perceptrón dio 0 (es decir, subestimó), aumentamos los pesos de las entradas que contribuyeron a la subestimación y/o aumentamos el sesgo.
• Si la salida esperada era 0 pero el perceptrón dio 1 (es decir, sobreestimó), disminuimos los pesos de las entradas que contribuyeron a la sobreestimación y/o disminuimos el sesgo.

Este ajuste se hace de una manera específica, siguiendo una “regla de aprendizaje” (conocida como la regla de aprendizaje del perceptrón), para que el perceptrón converja y aprenda a clasificar correctamente los datos que ha visto. Repetimos este proceso miles o millones de veces con diferentes ejemplos hasta que el perceptrón sea lo suficientemente preciso.

Limitaciones del Perceptrón Original

Si bien el perceptrón fue un avance revolucionario, tenía una limitación importante: solo podía resolver problemas que eran linealmente separables. Imagina un gráfico con puntos rojos y azules. Si puedes dibujar una línea recta en el gráfico que separe perfectamente todos los puntos rojos de todos los puntos azules, entonces el problema es linealmente separable. El perceptrón es excelente para esto.

Pero, ¿qué pasa si los puntos rojos y azules están mezclados de tal manera que no puedes separarlos con una sola línea recta? (Piensa en una “X” donde los puntos rojos están en los brazos superior izquierdo y superior derecho, y los azules en los brazos inferior izquierdo y inferior derecho). El perceptrón simple no puede resolver este tipo de problemas. Esta limitación llevó a una pausa en la investigación de redes neuronales durante años, conocida como el “invierno de la IA”.

Más Allá del Perceptrón Simple: Redes Multicapa

La solución a la limitación del perceptrón fue la creación de redes neuronales multicapa (también conocidas como Multi-Layer Perceptrons o MLPs). Estas redes apilan múltiples perceptrones en diferentes “capas”:

• Capa de Entrada: Recibe los datos originales.
• Capas Ocultas: Aquí es donde ocurre la magia real. Múltiples perceptrones trabajan juntos, procesando la información de la capa anterior y extrayendo características más complejas. Cada perceptrón en estas capas puede detectar un patrón diferente.
• Capa de Salida: Produce la predicción final.

Al combinar muchos perceptrones en capas, con funciones de activación más sofisticadas (no solo el simple “sí/no”), las redes neuronales pueden aprender a resolver problemas increíblemente complejos y no linealmente separables. Aquí es donde entra en juego las famosas matrices.

El perceptrón, en su simplicidad, es la semilla de la que han brotado las maravillas de la inteligencia artificial moderna. Aunque no puede resolver todos los problemas por sí solo, su concepto de entradas ponderadas, suma y activación binaria sentó las bases para el desarrollo de arquitecturas mucho más complejas.

Entender el perceptrón no es solo aprender una pieza de la historia de la IA; es comprender el principio fundamental de cómo las máquinas pueden aprender a tomar decisiones a partir de los datos. Desde este humilde comienzo, hemos llegado a las redes neuronales profundas que hoy reconocen rostros, traducen idiomas y conducen vehículos. El perceptrón redes neurales, con sus vectores, pesos y producto escalar, fue la primera y crucial chispa.