
Nel contesto del game developement, la generazione procedurale del terreno è una tecnica che utilizza algoritmi specifici per creare automaticamente ambienti di gioco (montagne, colline, isole…) in modo dinamico, ovvero senza che gli sviluppatori debbano realizzarli a mano.
La generazione procedurale è particolarmente comuni in giochi in cui si vuole fare in modo che il giocatore viva un’esperienza diversa ad ogni partita. È infatti molto comune in quei videogiochi in cui il gameplay è incentrato sull’esplorazione, la rigiocabilità, la scoperta e la varietà del mondo di gioco. Essa non è limitata solo al terreno o al mondo di gioco, ma può anche essere estesa a grafiche, effetti sonori, animazioni, questlines e molto altro.
In questo articolo cerchiamo di capire meglio come funziona la generazione procedurale del terreno, osservando un esempio funzionante realizzato in Unity.
Il funzionamento di un generatore procedurale, ad alto livello
Un generatore procedurale per un mondo di gioco è essenzialmente un algoritmo che prende in input un numero intero, detto seed, e eventualmente altri parametri utili, e genera il mondo di gioco in maniera automatica sulla base dei parametri passati e del seed.
Il seed è utilizzato per garantire che il mondo sia generato in maniera deterministica: a parità di seed e parametri, il mondo generato dall’algoritmo sarà sempre identico.
Il seed è infatti utilizzato per inizializzare uno o più generatori di numeri pseudo-casuali, che, in quanto tali, generano numeri che sembrano casuali, ma che sono in realtà completamente deterministici. Attraverso lunghe serie di trasformazioni, questi dati determinano la struttura del mondo di gioco.
Questo può non sembrare molto interessante, ma offre in realtà un grande vantaggio: un mondo generato proceduralmente non ha bisogno di essere memorizzato localmente. Questo significa che anche mondi di dimensioni “infinite” sono tranquillamente realizzabili e riproducibili.
Vediamo allora più nel dettaglio una semplice implementazione per un generatore procedurale per il terreno di un generico mondo di gioco.
Perlin noise – che cos’è e come funziona
Il Perlin noise è un tipo di rumore sviluppato da Ken Perlin nel 1983. Si tratta di una funzione pseudo-casuale che restituisce valori numerici compresi tra -1 e 1 che variano in maniera graduale e “naturale” tra loro.

Il Perlin noise è implementato creando una griglia sui cui vertici vengono definiti dei vettori di lunghezza unitaria con direzione scelta in maniera pseudo-casuale. Questi vettori sono detti “gradienti“.
Per ogni singolo punto all’interno della griglia si calcola poi il vettore di offset rispetto ai vertici della cella della griglia in cui si trova il punto (che in 2D sono 4).
Si calcola poi il prodotto scalare tra i vettori di offset e i gradienti dei rispettivi vertici. Si ottengono così degli scalari che sono poi “fusi” insieme tramite interpolazione, ottenendo il risultato sopra.
Perlin noise – utilizzi
La maggior parte dei game engine mettono a disposizione funzioni come il Perlin noise pronte per l’uso. Tipicamente l’output di queste funzioni è normalizzato nel range 0-1.
Unity, ad esempio, mette a disposizione la funzione PerlinNoise nella classe Mathf, definita come:
public static float PerlinNoise(float x, float y);Code language: PHP (php)Questa funzione prende in input i punti di sample x e y, da cui sarà calcolato il valore in output.
La chiave di moltissimi algoritmi di generazione procedurale del terreno è utilizzare il valore in output dal Perlin noise come offset verticale per i vertici di un piano.
Possiamo infatti costruire un piano suddiviso tante volte in modo da essere costituito da tante celle della stessa dimensione allineate a formare una griglia. Calcolando il Perlin noise in corrispondenza delle coordinate dei vertici della griglia, otteniamo un valore per ciascun vertice. Questo valore è utilizzato per determinare di quanto alzare il vertice da cui è stato calcolato.
In questo modo il Perlin noise viene “proiettato” sul terreno, alzandolo e facendogli assumere una forma ondulatoria, simile a un paesaggio collinare.
Si noti che il metodo Mathf.PerlinNoise offerto da Unity è una funzione deterministica: dato lo stesso input, restituisce sempre lo stesso valore, ma non consente di specificare un seed in maniera diretta, perché non si basa su un generatore di numeri pseudo-casuali interno.
È comunque possibile simulare un comportamento simile al seed introducendo un offset costante nelle coordinate di input. Ad esempio, usando x + seedOffsetX e y + seedOffsetY, è possibile ottenere varianti del terreno generate in modo consistente a partire da un seed arbitrario.
Generazione della mesh
Per questo esempio rimaniamo su qualcosa di molto semplice. La prima cosa da fare è costruire la mesh di partenza che poi deformeremo utilizzando il Perlin noise.
La mesh in questione non è altro che un piano suddiviso un certo numero di volte.
Definiamo allora due variabili:
Scale: specifica la dimensione del piano (per questo esempio supponiamo di forma quadrata)Resolution: il numero di suddivisioni del piano
In Unity una mesh è definita da 3 ingredienti:
- Un array di
Vector3(vertices), che rappresentano i vertici della mesh - Un array di
int(triangles), che rappresentano i triangoli di cui è costituita la mesh - Un array di
Vector2(uvs), che rappresenta la mappa uv della mesh
La generazione procedurale e l’interazione con ambienti di gioco generati proceduralmente funziona quasi sempre operando su questi dati. Il codice per generare il piano è il seguente:
using System;
using UnityEngine;
[ExecuteInEditMode]
public class worldGenerator : MonoBehaviour
{
public int scale = 20;
public int resolution = 10;
void Awake()
{
Generate();
}
void OnValidate()
{
Generate();
}
void Generate()
{
Mesh mesh = new Mesh();
mesh.indexFormat = UnityEngine.Rendering.IndexFormat.UInt32;
int vertexCount = (resolution + 1) * (resolution + 1);
Vector3[] vertices = new Vector3[vertexCount];
Vector2[] uvs = new Vector2[vertexCount];
for (int y = 0; y <= resolution; y++)
{
for (int x = 0; x <= resolution; x++)
{
int index = x + y * (resolution + 1);
Vector2 normalizedPosition = new Vector2((float)x / resolution, (float)y / resolution);
Vector2 worldPosition = normalizedPosition * scale;
vertices[index] = new Vector3(worldPosition.x, 0f, worldPosition.y);
uvs[index] = new Vector2(normalizedPosition.x, normalizedPosition.y);
}
}
int[] triangles = new int[resolution * resolution * 6];
int i = 0;
for (int y = 0; y < resolution; y++)
{
for (int x = 0; x < resolution; x++)
{
int vertexIndex = x + y * (resolution + 1);
triangles[i] = vertexIndex;
triangles[i + 1] = vertexIndex + resolution + 1;
triangles[i + 2] = vertexIndex + 1;
triangles[i + 3] = vertexIndex + 1;
triangles[i + 4] = vertexIndex + resolution + 1;
triangles[i + 5] = vertexIndex + resolution + 2;
i += 6;
}
}
mesh.vertices = vertices;
mesh.triangles = triangles;
mesh.uv = uvs;
mesh.RecalculateNormals();
GetComponent<MeshFilter>().mesh = mesh;
}
}
Code language: C# (cs)Con questo codice:
- Specifichiamo la posizione dei vertici disponendoli su una griglia quadrata che copre l’intero piano.
- Specifichiamo gli uv normalizzando le coordinate dei vertici.
- Definiamo i triangoli che costituiscono la mesh indicando come connettere i vari vertici tra loro per formare ogni singolo triangolo.
- Assegnamo i dati così prodotti alla mesh creata e la associamo al MeshFilter dell’oggetto su cui stiamo lavorando.
Applichiamo il Perlin noise
A questo punto possiamo applicare il Perlin noise. Per prima cosa, deformiamo la mesh usando Mathf.PerlinNoise: ci basta specificare come coordinata y nella definizione dei vertici il valore in output dal Perlin noise calcolato in corrispondenza di ciascun vertice:
vertices[index] = new Vector3(worldPosition.x, Mathf.PerlinNoise(normalizedPosition.x, normalizedPosition.y), worldPosition.y);
Code language: JavaScript (javascript)Con questa modifica il piano viene deformato a tutti gli effetti, ma di poco: Mathf.PerlinNoise restituisce infatti valori compresi tra 0 e 1. Possiamo definire una variabile height da usare per scalarne il risultato e avere così una deformazione maggiore. Per comodità, definiamo anche una funzione getElevation(float x, float y) che ritorni la y da assegnare a ciascun vertice. La logica di generazione sarà specificata al suo interno.
float getElevation(float x , float y) {
return Mathf.PerlinNoise(x , y) * height;
}
...
vertices[index] = new Vector3(worldPosition.x, getElevation(normalizedPosition.x, normalizedPosition.y), worldPosition.y);
Code language: JavaScript (javascript)Si noti che, pur passando a getElevation le coordinate normalizzate, sarebbe stato corretto anche passare le coordinate effettive dei vertici (e, anzi, solitamente si fa così). Ho preferito fare in questo modo per mantenere la logica che garantisce l’indipendenza tra la deformazione del terreno e il valore della variabile scale visibile all’esterno della funzione.
Poiché le coordinate sono sempre normalizzate in un range 0-1, il Perlin noise è calcolato su coordinate con la stessa magnitudine, indipendentemente dalle dimensioni della mappa. Questo garantisce generazioni identiche anche con dimensioni della mappa molto diverse. La variabile height, volendo, può essere scalata dinamicamente in modo da mantenere anche l’altezza della deformazione costante su scale diverse.
Perlin noise e ottave
Il terreno che abbiamo ottenuto nel paragrafo precedente è abbastanza noioso e piuttosto artificiale. Non assomiglia molto a una catena montuosa e manca di dettagli.
Per risolvere il problema dobbiamo trovare un modo per aggiungere imperfezioni ai valori ottenuti dal Perlin noise. Una tecnica usatissima per fare proprio questo è la tecnica delle ottave.
Quello che si fa è usare come rumore non uno, ma più Perlin noise sommati tra di loro.
Il concetto riprende le ottave musicali. Questa tecnica prevede di partire con un Perlin noise semplice, con frequenza bassa e ampiezza alta.
- Per frequenza si intende quanto velocemente variano i valori del Perlin noise
- Per ampiezza si intende quanto grandi sono questi valori
A partire da una frequenza e un’ampiezza iniziale, si generano via via Perlin noise con frequenza doppia ma ampiezza dimezzata. Ciascun Perlin noise è poi sommato al precedente, e il processo viene ripetuto un certo numero, finito, di volte. Ciascun passaggio aumenta il dettaglio del rumore di output, permettendo quindi al nostro paesaggio di assumere un aspetto ben più naturale.
Implementiamo allora una funzione che calcoli il Perlin noise con un certo numero di ottave:
float octaveNoise(float x, float y, int octaveCount, float baseFrequency , float baseAmplitude, float lacunarityValue, float persistenceValue)
{
float frequency = baseFrequency;
float amplitude = baseAmplitude;
float totalAmplitude = 0;
float value = 0;
for (int i = 0; i < octaveCount; i++)
{
value += Mathf.PerlinNoise(x * frequency, y * frequency) * amplitude;
totalAmplitude += amplitude;
frequency *= lacunarityValue;
amplitude *= persistenceValue;
}
return value / totalAmplitude;
}
Code language: HTML, XML (xml)Si noti che qui specifichiamo anche di quanto via via scalare frequenza e ampiezza, rispettivamente tramite lacunarityValue e persistenceValue. Il valore calcolato come somma delle ottave, prima di essere ritornato dalla funzione, viene normalizzato tramite divisione per la somma delle ampiezze di ogni ottava.
Ora possiamo usare questa versione del Perlin noise nel nostro generatore procedurale:
float getElevation(float x , float y)
{
return octaveNoise(x, y, terrainOctaves, terrainBaseFrequency, terrainBaseAmplitude, terrainLacunarity, terrainPersistence) * height;
}Code language: JavaScript (javascript)Un po’ di colore
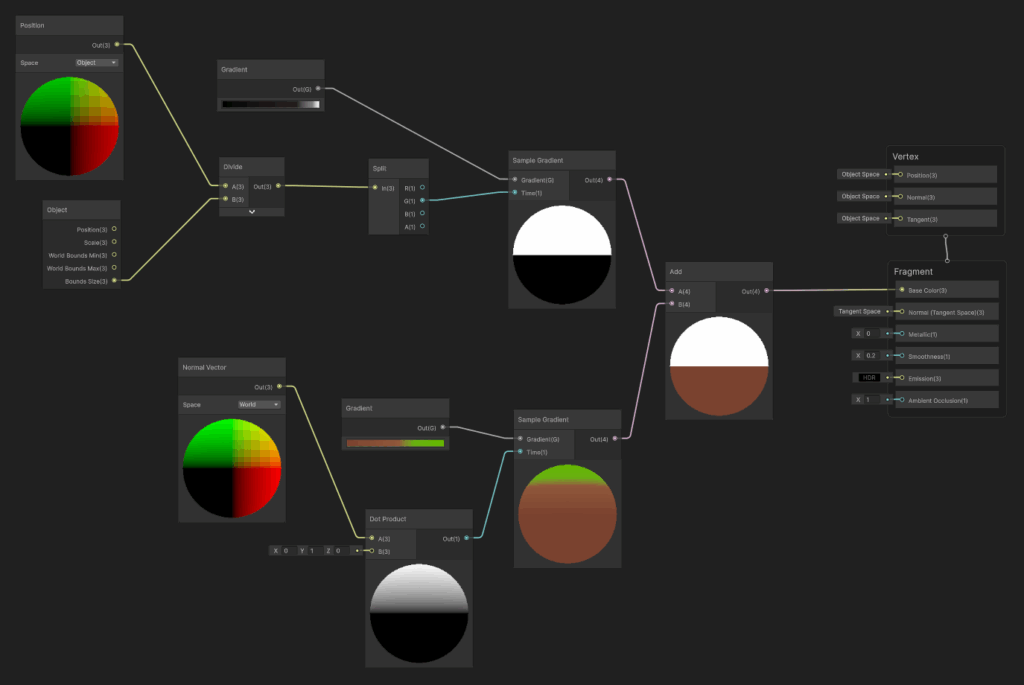
Ora che abbiamo un terreno che ha un aspetto accettabile, possiamo divertirci a colorarlo come preferiamo. Per fare ciò ho creato un piccolo shader tramite shader graph usato dal materiale associato al terreno.
Il compito di questo shader è colorare di verde le zone più pianeggianti, di marrone le zone di montagna e le zone pendenti, e di bianco le zone più alte, come se le cime delle montagne siano coperte di neve.
Per colorare in maniera diversa zone pianeggianti e zone montuose, calcoliamo il prodotto scalare tra la normale del terreno e il vettore unitario che rappresenta l’asse verticale del mondo di gioco.
Fare ciò ci restituisce un valore che è pari a 1 se i due vettori puntano entrambi nello stesso verso, e minore di uno se puntano in direzioni diverse. Man mano che i vettori diventano ortogonali, il prodotto scalare approccia zero.
Questo fa sì che i punti del terreno più in pendenza assumano un colore marrone, mentre i punti meno in pendenza si colorino di verde.
Per fare in modo che le cime delle montagne siano innevate, possiamo semplicemente valutare la posizione di ciascun vertice in relazione al bounding box del terreno, e aggiungere al colore derivante dal procedimento spiegato sopra un colore bianco che è tanto più chiaro quanto più in alto si trova il vertice rispetto al bounding box. Questo sistema è ottimo quando siamo sicuri che il terreno assuma un certo valore massimo in prossimità della cima di una montagna, ma va adattato meglio nel caso in cui si prevedano chunk di terreno pianeggianti, eventualmente inserendo un threshold assoluto o in altro modo.
Lo shader graph finale è il seguente:
E il risultato complessivo è questo:

Considerazioni aggiuntive
Questo articolo funge da esempio base per quello che l’universo della generazione procedurale del terreno. Ci sarebbe moltissimo da aggiungere a un sistema del genere, ma si tratta pur sempre di un punto di partenza utile per comprendere i concetti fondamentali di queste metodologie.
A questo punto sarebbe interessante riscrivere la generazione del terreno utilizzando un vertex shader, gestire la generazione di chunk e biomi, approfondire tecniche di ottimizzazione e di LOD e molto altro. Le possibilità sono infinite!




