
L’apprendimento non supervisionato è una tecnica di machine learning che non è guidata dagli esseri umani.
Nell’apprendimento supervisionato, i data scientists raccolgono i dati da una fonte. Questi dati sono etichettati, il che significa che i data scientists li utilizzano per fare previsioni. In altre parole, conoscono la risposta corretta a cui un modello di machine learning deve arrivare, quindi valutano quanto sia buono quel modello nel raggiungere la risposta corretta.
Quindi, nell’apprendimento supervisionato, i data scientists utilizzano i dati che hanno per addestrare modelli di machine learning in modo tale che possano fare previsioni accurate su dati che il modello non ha mai visto prima.
L’apprendimento non supervisionato, invece, funziona con un processo diverso. C’è comunque un intervento umano, ovviamente. Ad esempio, per raccogliere e pulire i dati. Tuttavia, i data scientists utilizzano l’apprendimento non supervisionato per esplorare la struttura dei loro dati ed estrarre informazioni significative da essi.
Ci sono due tipi di apprendimento non supervisionato:
- Clustering.
- Riduzione della dimensionalità.
Questo articolo è un’introduzione all’analisi dei gruppi per trovare informazioni significative nei dati.
Introduzione all’analisi per cluster
E’ una tecnica di esplorazione dei dati – spesso chiamata tecnica di pattern discovery – che ci consente di organizzare i dati in sottoinsiemi significativi – chiamati clusters – senza avere conoscenza preventiva dell’appartenenza dei dati a gruppi specifici.
Dal punto di vista pratico, alimentiamo un modello di machine learning con i dati che abbiamo e esso sarà in grado di individuare le connessioni significative tra i dati, consentendo la suddivisione in sottogruppi.
Ecco come una tecnica mostrerebbe i cluster su un dato insieme di dati:
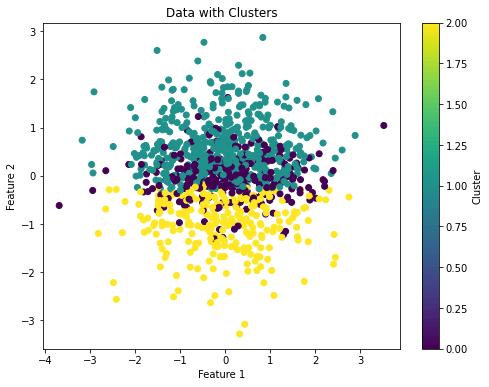
L’immagine sopra mostra che l’algoritmo ha individuato tre cluster nell’insieme di dati fornito e li rappresenta con colori differenti.
Quindi, ciascun cluster che emerge durante l’analisi definisce un gruppo di oggetti che condividono un certo grado di somiglianza. Questi oggetti sono anche dissimili dagli oggetti presenti negli altri cluster, ed è per questo che si tratta di un processo non supervisionato.
Pertanto, l’analisi è un’ottima metodologia per strutturare le informazioni e significative presenti nei dati.
In particolare, può essere utilizzata con una moltitudine di obiettivi in mente. Ad esempio, può essere utilizzata dai marketer per scoprire gruppi di clienti basati sui loro interessi.
Oppure, può anche essere utilizzata dai data scientists per definire le labels di un dataset da utilizzare per fare predizioni. In altre parole, ci sono casi in cui le labels non sono chiare o sono sconosciute e possiamo utilizzarlo per definirle.
Le tecniche di analisi dei gruppi tipiche sono:
- K-means.
- Hierarchical.
- DBSCAN.
Questo articolo si concentra sui primi due.
Lettura consigliata: Come sviluppare il tuo Chatbot con Python e ChatterBot partendo da zero
Un’introduzione ai popolari algoritmi in Python
In questa sezione, descriveremo come funzionano il k-mean e lo hierarchical. Implementeremo anche esempi in Python per mostrare come usarli.
K-Means clustering
L’algoritmoin questione appartiene a una categoria chiamata basata su prototipi.
In questa categoria, un cluster è rappresentato come un prototipo, che di solito è il centroide (la media) dei punti simili nel caso di caratteristiche continue, o il medoide (il più rappresentativo o il punto che minimizza la distanza da tutti gli altri punti che appartengono a un cluster specifico) nel caso di caratteristiche categoriche.
L’algoritmo è molto efficace nell’identificare clusters con una forma sferica, ma uno dei suoi svantaggi è che dobbiamo specificare il numero di cluster, k, in anticipo.
Una non corretta di k può portare a una scarsa performance dell’analisi dei gruppi , ma esistono metodi per valutare la qualità di un cluster che ci aiutano a determinare il numero ottimale di cluster, k.
Quando ci riferiamo alla “forma sferica” di un cluster, intendiamo che i punti dati all’interno di un cluster sono distribuiti in modo simile a una sfera tridimensionale (o a un cerchio bidimensionale). In altre parole, i punti nel cluster sono strettamente raggruppati intorno a un punto centrale, e le distanze da questo punto centrale ai punti dati sono approssimativamente uguali in tutte le direzioni.
Ecco come appare una distribuzione dei dati sferica e non sferica in due dimensioni:
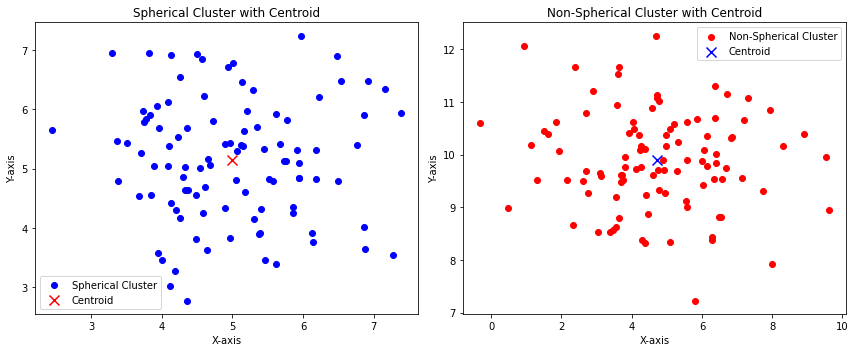
L’immagine sopra mostra che:
- I punti blu sono, in qualche modo, distribuiti con distanze speculari rispetto al centro della distribuzione (il centroide). Questo può rappresentare un cluster sferico.
- I punti rossi non sono distribuiti con distanze speculari rispetto al centro della distribuzione (il centroide). Questo può rappresentare un cluster non sferico.
Ora vogliamo estendere il concetto legato alla distanza. L’esempio sopra mostra solo un cluster allo scopo di visualizzare una distribuzione sferica e una non sferica.
Creiamo quindi un dataset composto da 150 punti generati casualmente raggruppati in tre sottogruppi. Possiamo usare il seguente codice per farlo:
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
# Create 3 clusters with 150 randomly generated data points and 2 features
X,y = make_blobs(n_samples=150, n_features=2, centers=3, cluster_std=0.5, shuffle=True, random_state=0)
# Plot the points as a scatterplot
plt.scatter(X[:,0], X[:, 1], c="white", marker="o", edgecolor="black", s=50)
# Write labels, show grid and plot
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.grid()
plt.tight_layout()
plt.show()Code language: PHP (php)Otteniamo:
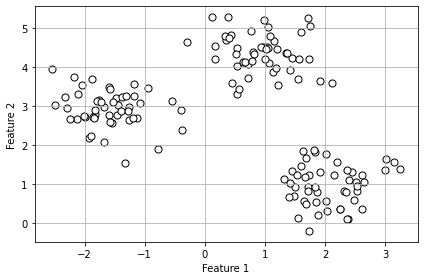
Ora, nelle applicazioni reali, non sappiamo in quanti cluster possono essere suddivisi i dati, che è il valore k che dobbiamo trovare, come abbiamo detto prima. Per fare ciò, possiamo seguire questi passaggi:
- Scegli k centroidi casuali dagli esempi come centri iniziali del cluster.
- Assegna ogni esempio al centroide più vicino 𝜇(i),j ∊ [1,…,k]
- Sposta i centroidi al centro degli esempi che gli sono stati assegnati.
- Ripeti i passaggi 2 e 3 finché le assegnazioni dei cluster non cambiano o non viene raggiunta una tolleranza definita dall’utente o un numero massimo di iterazioni.
Ora, come misuriamo la similarità tra oggetti?
Se stessimo valutando i colori di alcune auto, ad esempio, l’occhio umano potrebbe dire che un’auto arancione sia simile ad una rossa. Ma come possiamo definire la similarità in matematica?
Possiamo definire la similarità come l’opposto della distanza. Una metrica di distanza, infatti, quantifica la dissimilarità o la distanza tra due punti dati. Più è piccola la distanza tra due punti, più questi sono simili. Più è grande la distanza, meno sono simili.
Quindi, in questo senso, “similarità” e “distanza” sono inversamente correlati: una distanza più piccola implica una maggiore similarità, mentre una distanza più grande implica una minore similarità.
Una distanza comunemente utilizzata nell’analisi dei gruppi con feature continue è la distanza Euclidea al quadrato tra due punti, x e y:
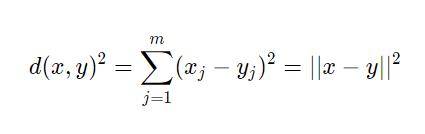
Quindi, sulla base di questa metrica, può essere descritto come un problema di ottimizzazione: è un algoritmo iterativo che minimizza la somma degli errori quadratici all’interno di un cluster.
Per semplicità, non andiamo oltre con la matematica in questo articolo.
Proseguiamo implementando un algoritmo in Python:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.cluster import KMeans
# Generate data
X, y = make_classification(n_samples=1000, n_features=20, random_state=42)
# Create a K-Means clustering model
kmeans = KMeans(n_clusters=3, random_state=42)
# Fit the model to your data
cluster_labels = kmeans.fit_predict(X)
# Create a scatter plot for the first two features
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=cluster_labels, cmap='viridis')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Data with Clusters')
plt.colorbar(label='Cluster')
plt.show()Code language: PHP (php)E otteniamo l’immagine che abbiamo visto all’inizio dell’articolo:

Dunque, con from sklearn.cluster import KMeans importiamo il modello k-means da sklearn. Poi, possiamo gestire il numero di cluster modificando il parametro n_clusters.
Lettura consigliata: Librerie Python per Data Science: una guida completa
Hierarchical clustering
E’ una tecnica utilizzata per raggruppare i punti dati in cluster nidificati o in una struttura gerarchica. È particolarmente utile quando vogliamo esplorare l’organizzazione dei dati a vari livelli di granularità.
Due grandi vantaggi dello hierarchical sono:
- La possibilità di tracciare il dendrogramma. Questa è la visualizzazione di binario e può aiutare con l’interpretazione dei risultati.
- Non è necessario specificare il numero di cluster.
I due principali approcci sono:
- Agglomerative. Iniziamo con ogni esempio come un singolo cluster e uniamo le coppie di cluster più vicine finché non rimane un solo cluster.
- Divisive.
- Iniziamo con un cluster che comprende il set di dati completo e dividiamo iterativamente il cluster in cluster più piccoli finché ciascun cluster non contiene un solo esempio.
In questo articolo, considereremo l’agglomerative.
I due algoritmi standard per l’agglomerative sono:
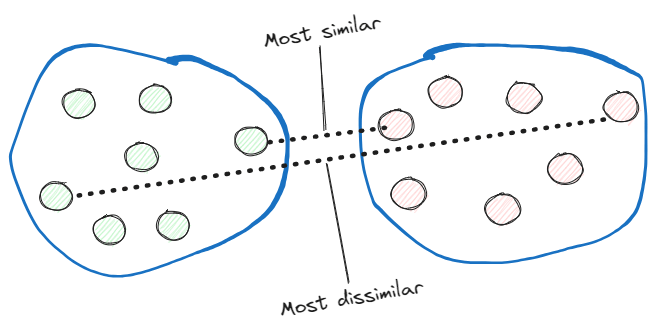
- Single linkage. Questo calcola le distanze tra i membri più simili di ciascuna coppia di cluster e unisce i due cluster per i quali la distanza tra i membri più simili è la più piccola.
- Complete linkage. Invece di confrontare i membri più simili, confronta quelli più dissimili per eseguire l’unione.
Implementiamo un agglomerative hierarchical con l’approccio complete linkage in Python:
import numpy as np
from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt
# Create a synthetic dataset with 20 features and 200 data points
np.random.seed(0)
X = np.random.rand(200, 20)
# Perform hierarchical clustering with complete linkage
linkage_matrix = linkage(X, method='complete', metric='euclidean')
# Plot the dendrogram
plt.figure(figsize=(12, 6))
dendrogram(linkage_matrix, truncate_mode='lastp', p=20, leaf_rotation=90., leaf_font_size=8., show_contracted=True)
plt.title('Hierarchical Clustering Dendrogram with Complete Linkage')
plt.xlabel('Data Points')
plt.ylabel('Distance')
plt.show()Code language: PHP (php)Abbiamo creato un dataset con 200 punti creati randomicamente e 20 features con il metodo np.random.rand(). Poi abbiamo creato lo hierarchical cluster con li metodo linkage() dalla libreria SciPy.
Dal codice sopra otteniamo il seguente dendrogramma:
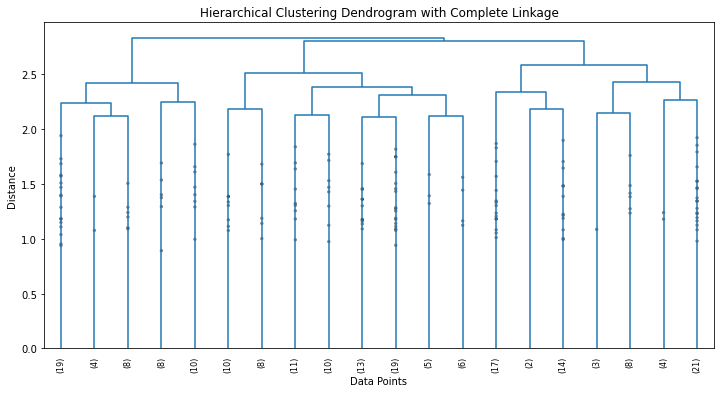
Quindi, un dendrogramma è un diagramma ad albero utilizzato per visualizzare le relazioni tra i punti dati in un dataset. In particolare, ci mostra la gerarchia di come i punti dati siano raggruppati in base alla loro somiglianza.
Ecco come interpretare il dendrogramma ottenuto nell’esempio sopra:
- Linee verticali(Branches). Inizialmente rappresentano punti dati individuali. Man mano che saliamo nel dendrogramma, queste linee iniziano a fondersi in gruppi.
- Linee orizzontali (Links). Le linee orizzontali che collegano le linee verticali rappresentano l’unione dei cluster. L’altezza di queste linee corrisponde alla dissomiglianza tra i cluster uniti. Più alta è la linea, maggiore è la dissomiglianza tra i cluster da unire.
- Clusters. Le foglie del dendrogramma rappresentano i punti presi singolarmente. Man mano che saliamo nel dendrogramma, i cluster si formano unendo punti dati o cluster più piccoli. I rami nella parte inferiore del dendrogramma rappresentano il livello più alto di analisi dei gruppi (singoli punti dati), mentre i rami ai livelli più alti rappresentano cluster più grandi formati unendo quelli più piccoli.
- Tagliare il dendrogramma. Per determinare il numero di cluster, possiamo tracciare una linea orizzontale (chiamata “taglio”) ad una certa altezza sul dendrogramma. Il numero di cluster è determinato dal numero di volte in cui la linea orizzontale interseca le linee verticali. Ogni punto di intersezione corrisponde ad un cluster.
Possiamo tagliare un dendrogramma tenendo a mente le seguenti idee:
- Se tagliamo il dendrogramma ad alto livello (linea orizzontale alta), otteniamo un numero minore di cluster più grandi, che sono più dissimili tra loro.
- Se tagliamo il dendrogramma ad un livello più basso (breve linea orizzontale), otteniamo un numero maggiore di cluster più piccoli e più simili tra loro.
Nel nostro caso, vogliamo quelli più dissimili poiché utilizziamo il metodo complete linkage.
Possiamo, quindi, sceglierne tre come numero per i cluster.
Ora possiamo usare scikit-learn per applicare un agglomerative hierarchical cluster con 3 cluster:
import numpy as np
from scipy.cluster.hierarchy import linkage, dendrogram
from sklearn.cluster import AgglomerativeClustering
import matplotlib.pyplot as plt
# Create dataset with 20 features and 200 data points
np.random.seed(0)
X = np.random.rand(200, 20)
# Perform hierarchical clustering with complete linkage
linkage_matrix = linkage(X, method='complete', metric='euclidean')
# Specify the desired number of clusters
n_clusters = 3
# Create an Agglomerative Clustering model
agg_cluster = AgglomerativeClustering(n_clusters=n_clusters)
# Fit the model to the data and get cluster labels
cluster_labels = agg_cluster.fit_predict(X)
# Plot the data with cluster labels
plt.scatter(X[:, 0], X[:, 1], c=cluster_labels, cmap='viridis')
plt.title(f'Agglomerative Clustering with {n_clusters} Clusters')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.colorbar(label='Cluster')
plt.show()Code language: PHP (php)E otteniamo:
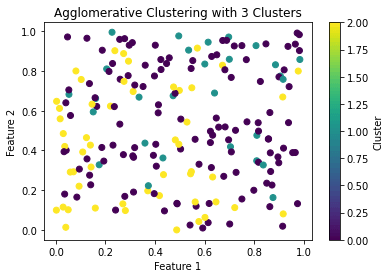
Lettura consigliata: Python e DataBricks: la giusta accoppiata per dominare i dati
Conclusioni
In questo articolo, abbiamo descritto una tecnica di apprendimento non supervisionato.
Abbiamo anche mostrato due metodologie diverse con implementazioni in Python:
- K-means.
- Hierarchical.
Queste sono le metodologie giuste per trovare strutture nascoste e connessioni tra i dati durante la fase di analisi esplorativa dei dati.
Fonti:
[1] Machine Learning With PyTorch and Scikit-Learn – Sebastian Raschka, Yuxi Liu, Vahid Mirjalili
